Was ist ein Trie ? 🤔
Trie ist eine Baumbasierte Datenstruktur, die in der Informatik verwendet wird, um das Suchen von Zeichenkette zu vereinfachen
Erfinder dieser Datenstruktur ist der Physiker Edward Fredkin. Dabei gibt es drei Trie Formen: Standard Trie, Komprimierter Trie und Suffix Trie. Ein Standard Trie lässt sich folgenderweise definieren: Sei $S={S_{1},\dots ,S_{k}}$ eine Menge von Zeichenketten über dem Alphabet $∑$, sodass kein String in Präfix eines anderen String. Dadurch eignen sich Tries hervorragend fürs Pattern Matching und für die Autovervollständigung beim Schreiben von Texten oder von Quellcode. Es gibt jedoch einige wichtige Bemerkungen, die genannt werden sollten. Es sei eine Menge $S$ von $s$ Strings der Gesamtlänge $n$ aus einem Alphabet der Größe $k$ und die Länge des Strings $w$ :
- Es müssen alle Regeln einer Baumstruktur beachten werden
- Die Höhe von $T$ ist gleich lang des Längsten Strings in $S$,
- Die Anzahl der Knoten von $T$ ist $O(n)$,
- Bei der Suche nach $S$ beträgt $O(w)$.
Folgende Abbildung zeigt die Zeichnketten "bla", "bar", "blubb" und "foo" in einem unkomprimierten Trie. Die türkise Färbung an den Enden steht hier bei dafür, dass das gesuchte Wort identifiziert ist. In der Software würde hier eine abstrakte Datenstruktur definiert werden, die eine Boolsche Variable besitzt und "isEndOfWord" heißen könnte.
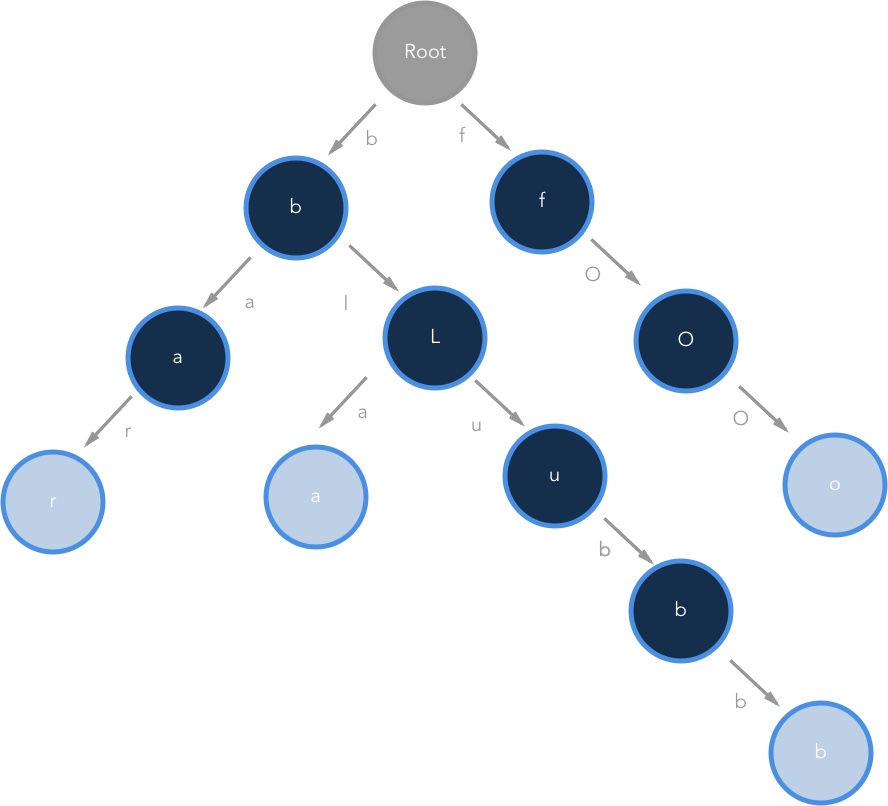
Bei der Suche des Baumes wird immer bei der Wurzel angefangen, anschließend wird das erste Zeichen, beispielsweise "b" bei der gesuchten Zeichenkette "bla" ab, mit den jeweils zwei unteren Kinderknoten. Wird bei einem der Kinderknoten eine Referenz bestätigt, wird dieser Kinderknoten besucht. Da das Zeichen b nun identifiziert ist wird mit dem Zeichen l fortgefahren. Dieser Vorgang wird solange wiederholt bis das Wort gefunden ist und alle Zeichen bis zum türkisen Knoten identifiziert sind. Nach Zeichenkette "ba" zu suchen wäre Aktuell nicht möglich, weil der Knoten A nicht türkis gefärbt ist. Dieser Knoten könnte auf true gesetzt werden bei "isEndOfWord", dann hätten wir die Zeichenkette "ba" hinzugefügt.
Die Effizienzklasse bei der Suche kann dann in Abhängigkeit von n abgeschätzt werden, wenn allen (die Anzahl der gespeicherten Strings) und alle möglichen Strings aus den Buchstaben a-z einer bestimmten Länge m gespeichert wurden, weil von dem längsten Fall ausgegangen werden kann. Eine höhere Komplexität kann nicht erreicht werden.